跳至主要內容

海量数据处理面试题

大数据中 TopK 问题的常用套路

对于海量数据到处理经常会涉及到 topK 问题。在设计数据结构和算法的时候，主要需要考虑的应该是当前算法（包括数据结构）跟给定情境（比如数据量级、数据类型）的适配程度，和当前问题最核心的瓶颈（如降低时间复杂度，还是降低空间复杂度）是什么。

首先，我们来举几个常见的 topK 问题的例子：

  1. 给定 100 个 int 数字，在其中找出最大的 10 个；
  2. 给定 10 亿个 int 数字，在其中找出最大的 10 个（这 10 个数字可以无序）；
  3. 给定 10 亿个 int 数字，在其中找出最大的 10 个（这 10 个数字依次排序）；
  4. 给定 10 亿个不重复的 int 数字，在其中找出最大的 10 个；
  5. 给定 10 个数组，每个数组中有 1 亿个 int 数字，在其中找出最大的 10 个；
  6. 给定 10 亿个 string 类型的数字，在其中找出最大的 10 个（仅需要查 1 次）；
  7. 给定 10 亿个 string 类型的数字，在其中找出最大的 k 个（需要反复多次查询，其中 k 是一个随机数字）。

上面这些问题看起来很相似，但是解决的方式却千差万别。稍有不慎，就可能使得 topK 问题成为系统的瓶颈。不过也不用太担心，接下来我会总结几种常见的解决思路，遇到问题的时候，大家把这些基础思路融会贯通并且杂糅组合，即可做到见招拆招。

堆排序法

这里说的是堆排序法，而不是快排或者希尔排序。虽然理论时间复杂度都是 O(nlogn)，但是堆排在做 topK 的时候有一个优势，就是可以维护一个仅包含 k 个数字的小顶堆（想清楚，为啥是小顶堆哦），当新加入的数字大于堆顶数字的时候，将堆顶元素剔除，并加入新的数字。

 int topK = 3;
 int[] vec = {4, 1, 5, 8, 7, 2, 3, 0, 6, 9};
 PriorityQueue < Integer > pq = new PriorityQueue < > (); // 小顶堆

 for (int x: vec) {
     pq.add(x);
     if (pq.size() > topK) {
         // 如果超出个数，则弹出堆顶（最小的）数据
         pq.poll();
     }
 }

 while (!pq.isEmpty()) {
     System.out.println(pq.poll()); // 输出依次为7, 8, 9
 }

类似快排法

快排大家都知道，针对 topK 问题，可以对快排进行改进。仅对部分数据进行递归计算。比如，在 100 个数字中，找最大的 10 个，第一次循环的时候，povit 被移动到了 80 的位置，则接下来仅需要在后面的 20 个数字中找最大的 10 个即可。

这样做的优势是，理论最优时间复杂度可以达到 O(n)，不过平均时间复杂度还是 O(nlogn)。需要说明的是，通过这种方式，找出来的最大的 k 个数字之间，是无序的。

public static int partition(int[] arr, int begin, int end) {
    int left = begin;
    int right = end;
    int pivot = arr[begin];

    while (left < right) {
        while (left < right && arr[right] >= pivot) {
            right--;
        }
        while (left < right && arr[left] <= pivot) {
            left++;
        }
        if (left < right) {
            swap(arr, left, right);
        }
    }

    swap(arr, begin, left);
    return left;
}

public static void partSort(int[] arr, int begin, int end, int target) {
    if (begin >= end) {
        return;
    }

    int pivot = partition(arr, begin, end);
    if (target < pivot) {
        partSort(arr, begin, pivot - 1, target);
    } else if (target > pivot) {
        partSort(arr, pivot + 1, end, target);
    }
}

public static int[] getMaxNumbers(int[] arr, int k) {
    int size = arr.length;
    // 把求最大的k个数，转换成求最小的size-k个数字
    int target = size - k;
    partSort(arr, 0, size - 1, target);
    return Arrays.copyOfRange(arr, target, size);
}

private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

public static void main(String[] args) {
    int[] vec = {
        4, 1, 5, 8, 7, 2, 3, 0, 6, 9
    };
    int[] ret = getMaxNumbers(vec, 3);

    for (int x: ret) {
        System.out.println(x); // 输出7，8，9（理论上无序）
    }
}

使用 bitmap

有时候 topK 问题会遇到数据量过大，内存无法全部加载。这个时候，可以考虑将数据存放至 bitmap 中，方便查询。

比如，给出 10 个 int 类型的数据，分别是【13，12，11，1，2，3，4，5，6，7】，int 类型的数据每个占据 4 个字节，那这个数组就占据了 40 个字节。现在，把它们放到一个 16 个长度 bool 的 bitmap 中，结果就是【0，1，1，1，1，1，1，1，0，0，0，1，1，1，0，0】，在将空间占用降低至 4 字节的同时，也可以很方便的看出，最大的 3 个数字，分别是 11，12 和 13。

需要说明的是，bitmap 结合跳表一起使用往往有奇效。比如以上数据还可以记录成：从第 1 位开始，有连续 7 个 1；从第 11 位开始，有连续 3 个 1。这样做，空间复杂度又得到了进一步的降低。

这种做法的优势，当然是降低了空间复杂度。不过需要注意一点，bitmap 比较适合不重复且有范围（比如，数据均在 0 ～ 10 亿之间）的数据的查询。至于有重复数据的情况，可以考虑与 hash 等结构的混用。

使用 hash

如果遇到了查询 string 类型数据的大小，可以考虑 hash 方法。

举个例子，10 个 string 数字【"1001"，"23"，"1002"，"3003"，"2001"，"1111"，"65"，"834"，"5"，"987"】找最大的 3 个。我们先通过长度进行 hash，得到长度最大为 4，且有 5 个长度为 4 的 string。接下来再通过最高位值做 hash，发现有 1 个最高位为"3"的，1 个为"2"的，3 个为"1"的。接下来，可以通过再设计 hash 函数，或者是循环的方式，在 3 个最高位为"1"的 string 中找到最大的一个，即可找到 3 个最值大的数据。

这种方法比较适合网址或者电话号码的查询。缺点就是如果需要多次查询的话，需要多次计算 hash，并且需要根据实际情况设计多个 hash 函数。

字典树

字典树（trie）的具体结构和查询方式，不在这里赘述了，自行百度一下就有很多。这里主要说一下优缺点。

字典树的思想，还是通过前期建立索引信息，后期可以反复多次查询，并且后期增删数据也很方便。比较适合于需要反复多次查询的情况。

比如，反复多次查询字符序（例如：z>y>...>b>a）最大的 k 个 url 这种，使用字典树把数据存储一遍，就非常适合。既减少了空间复杂度，也加速了查询效率。

混合查询

以上几种方法，都是比较独立的方法。其实，在实际工作中，遇到更多的问题还是混合问题，这就需要我们对相关的内容，融会贯通并且做到活学活用。

举个例子：分布式服务跑在 10 台不同机器上，每台机器上部署的服务均被请求 10000 次，并且记录了个这 10000 次请求的耗时（耗时值为 int 数据），找出这 10*10000 次请求中，从高到低的找出耗时最大的 50 个。看看这个问题，很现实吧。我们试着用上面介绍的方法，组合一下来求解。

方法一

首先，对每台机器上的 10000 个做类似快排，找出每台机器上 top50 的耗时信息。此时，单机上的这 50 条数据是无序的。

然后，再将 10 台机器上的 50 条数据（共 500 条）放到一起，再做一次类似快排，找到最大的 50 个（此时应该这 50 个应该是无序的）。

最后，对这 50 个数据做快排，从而得到最终结果。

方法二

首先通过堆排，分别找出 10 台机器上耗时最高的 50 个数据，此时的这 50 个数据，已经是从大到小有序的了。

然后，我们依次取出 10 台机器中，耗时最高的 5 条放入小顶堆中。

最后，遍历 10 台机器上的数据，每台机器从第 6 个数据开始往下循环，如果这个值比堆顶的数据大，则抛掉堆顶数据并且把它加入，继续用下一个值进行同样比较。如果这个值比堆顶的值小，则结束当前循环，并且在下一台机器上做同样操作。

以上我介绍了两种方法，并不是为了说明哪种方法更好，或者时间复杂度更低。而是想说同样的事情有多种不同的解决方法，而且随着数据量的增加，可能会需要更多组合形式。在这个领域，数据决定了数据结构，数据结构决定了算法。

没有最好的方法，只有不断找寻更好的方法的程序员。适合的，才会是最好的。

接下来继续看一些实际的例子

统计不同号码的个数

题目描述

已知某个文件内包含大量电话号码，每个号码为8位数字，如何统计不同号码的个数？内存限制100M

思路分析

这类题目其实是求解数据重复的问题。对于这类问题，可以使用位图法处理

8位电话号码可以表示的范围为00000000～99999999。如果用1 bit表示一个号码，那么总共需要1亿个bit，总共需要大约10MB的内存。

申请一个位图并初始化为0，然后遍历所有电话号码，把遍历到的电话号码对应的位图中的bit设置为1。当遍历完成后，如果bit值为1，则表示这个电话号码在文件中存在，否则这个bit对应的电话号码在文件中不存在。

最后这个位图中bit值为1的数量就是不同电话号码的个数了。

那么如何确定电话号码对应的是位图中的哪一位呢？

可以使用下面的方法来做电话号码和位图的映射。

00000000 对应位图最后一位：0×0000…000001。
00000001 对应位图倒数第二位：0×0000…0000010（1 向左移 1 位）。
00000002 对应位图倒数第三位：0×0000…0000100（1 向左移 2 位）。
……
00000012 对应位图的倒数第十三位：0×0000…0001 0000 0000 0000（1 向左移 12 位）。

也就是说，电话号码就是1这个数字左移的次数。

具体实现

首先位图可以使用一个int数组来实现（在Java中int占用4byte）。

假设电话号码为 P，而通过电话号码获取位图中对应位置的方法为：

第一步，因为int整数占用4*8=32bit，通过 P/32 就可以计算出该电话号码在 bitmap 数组中的下标，从而可以确定它对应的 bit 在数组中的位置。

第二步，通过 P%32 就可以计算出这个电话号码在这个int数字中具体的bit的位置。只要把1向左移 P%32 位，然后把得到的值与这个数组中的值做或运算，就可以把这个电话号码在位图中对应的位设置为1。

以00000100号码为例。

  1. 首先计算数组下标，100 / 32 = 3，得到数组下标位3。
  2. 然后计算电话号码在这个int数字中具体的bit的位置，100 % 32 = 4。取余为0左移1位，故取余为4左移5位，得到000...000010000
  3. 将位图中对应的位设置为 1，即arr[2] = arr[2] | 000..00010000。
  4. 这就将电话号码映射到了位图的某一位了。

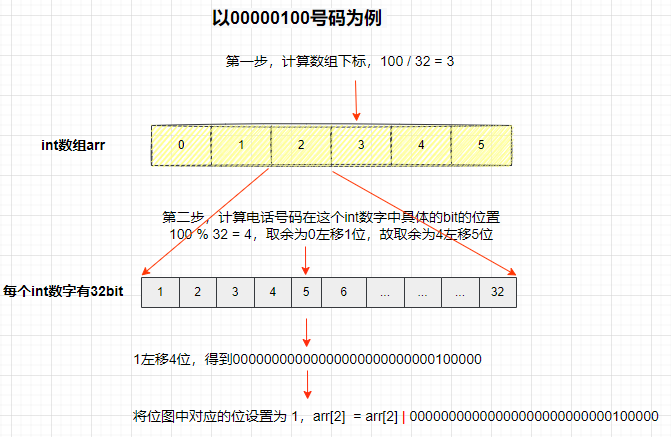
最后，统计位图中bit值为1的数量，便能得到不同电话号码的个数了。

出现频率最高的100个词

题目描述

假如有一个1G大小的文件，文件里每一行是一个词，每个词的大小不超过16byte，要求返回出现频率最高的100个词。内存大小限制是10M

解法1

由于内存限制，我们无法直接将大文件的所有词一次性读到内存中。

可以采用分治策略，把一个大文件分解成多个小文件，保证每个文件的大小小于10M，进而直接将单个小文件读取到内存中进行处理。

第一步，首先遍历大文件，对遍历到的每个词x，执行 hash(x) % 500，将结果为i的词存放到文件f(i)中，遍历结束后，可以得到500个小文件，每个小文件的大小为2M左右；

第二步，接着统计每个小文件中出现频数最高的100个词。可以使用HashMap来实现，其中key为词，value为该词出现的频率。

对于遍历到的词x，如果在map中不存在，则执行 map.put(x, 1)。

若存在，则执行 map.put(x, map.get(x)+1)，将该词出现的次数加1。

第三步，在第二步中找出了每个文件出现频率最高的100个词之后，通过维护一个小顶堆来找出所有小文件中出现频率最高的100个词。

具体方法是，遍历第一个文件，把第一个文件中出现频率最高的100个词构建成一个小顶堆。

如果第一个文件中词的个数小于100，可以继续遍历第二个文件，直到构建好有100个结点的小顶堆为止。

继续遍历其他小文件，如果遍历到的词的出现次数大于堆顶上词的出现次数，可以用新遍历到的词替换堆顶的词，然后重新调整这个堆为小顶堆。

当遍历完所有小文件后，这个小顶堆中的词就是出现频率最高的100个词。

总结一下，这种解法的主要思路如下：

  1. 采用分治的思想，进行哈希取余
  2. 使用HashMap统计每个小文件单词出现的次数
  3. 使用小顶堆，遍历步骤2中的小文件，找出词频top100的单词

但是很容易可以发现问题，在第二步中，如果这个1G的大文件中有某个词词频过高，可能导致小文件大小超过10m。这种情况下该怎么处理呢？

接下来看另外一种解法。

解法2

第一步：使用多路归并排序对大文件进行排序，这样相同的单词肯定是紧挨着的

多路归并排序对大文件进行排序的步骤如下：

① 分割文件：将文件按照顺序切分成大小不超过2m的小文件，总共500个小文件

② 内存内排序：对每个小文件使用内存进行排序。由于每个小文件的大小都在内存限制范围内，所以可以直接在内存中对它们进行排序。

③ 多路归并排序：使用一个大小为500大小的堆，对500个小文件进行多路排序，结果写到一个大文件中

其中第三步，对500个小文件进行多路排序的思路如下：

  • 初始化一个最小堆，大小就是有序小文件的个数500。堆中的每个节点存放每个有序小文件对应的输入流。
  • 通过比较堆顶的节点（即当前最小的词汇）来决定下一个写入大文件的词汇。
  • 如果堆顶的节点还有数据，就继续将其加入堆中；如果没有数据，就移除该节点。这个过程一直持续到所有小文件都被处理完毕。

第二步：

① 初始化小顶堆： 创建一个大小为100的小顶堆，用于存储出现频率最高的100个词汇。小顶堆的特点是堆顶是堆中最小的元素，这使得我们可以快速地替换掉频率较低的词汇。

② 遍历排序后的文件：逐个读取排序后的文件中的词汇，并进行计数。由于词汇已经排序，相同的词汇会连续出现，这使得计数变得简单。

③ 更新小顶堆：当遇到一个新的词汇时，比较其频率与小顶堆中频率最低的词汇（即堆顶）。如果新词汇的频率更高，则替换掉堆顶的词汇；如果频率更低或相等，则不做操作。这样，小顶堆中始终保持着出现频率最高的100个词汇。

解法2相对解法1，更加严谨，如果某个词词频过高或者整个文件都是同一个词的话，解法1不适用。

如何找出某一天访问百度网站最多的 IP？

题目描述

现有海量日志数据保存在一个超大文件中，该文件无法直接读入内存，要求从中提取某天访问百度次数最多的那个 IP。

解答思路

这道题只关心某一天访问百度最多的 IP，因此，可以首先对文件进行一次遍历，把这一天访问百度 IP 的相关信息记录到一个单独的大文件中。接下来采用的方法与上一题一样，大致就是先对 IP 进行哈希映射，接着使用 HashMap 统计重复 IP 的次数，最后计算出重复次数最多的 IP。

注：这里只需要找出出现次数最多的 IP，可以不必使用堆，直接用一个变量 max 即可。

方法总结

  1. 分而治之，进行哈希取余；

  2. 使用 HashMap 统计频数；

  3. 求解最大的 TopN 个，用小顶堆；求解最小的 TopN 个，用大顶堆。

如何在大量的数据中找出不重复的整数？

题目描述

在 2.5 亿个整数中找出不重复的整数。注意：内存不足以容纳这 2.5 亿个整数。

解答思路

方法一：分治法

与前面的题目方法类似，先将 2.5 亿个数划分到多个小文件，用 HashSet/HashMap 找出每个小文件中不重复的整数，再合并每个子结果，即为最终结果。

方法二：位图法

位图，就是用一个或多个 bit 来标记某个元素对应的值，而键就是该元素。采用位作为单位来存储数据，可以大大节省存储空间。

位图通过使用位数组来表示某些元素是否存在。它可以用于快速查找，判重，排序等。不是很清楚？我先举个小例子。

假设我们要对 [0,7] 中的 5 个元素 (6, 4, 2, 1, 5) 进行排序，可以采用位图法。0~7 范围总共有 8 个数，只需要 8bit，即 1 个字节。首先将每个位都置 0：

0 0 0 0 0 0 0 0

然后遍历 5 个元素，首先遇到 6，那么将下标为 6 的位的 0 置为 1；接着遇到 4，把下标为 4 的位 的 0 置为 1：

0 0 0 0 1 0 1 0

依次遍历，结束后，位数组是这样的：

0 1 1 0 1 1 1 0

每个为 1 的位，它的下标都表示了一个数：

for i in range(8):
    if bits[i] == 1:
        print(i)

这样我们其实就已经实现了排序。

对于整数相关的算法的求解，位图法是一种非常实用的算法。假设 int 整数占用 4B，即 32bit，那么我们可以表示的整数的个数为 232。

那么对于这道题，我们用 2 个 bit 来表示各个数字的状态：

  • 00 表示这个数字没出现过；
  • 01 表示这个数字出现过一次（即为题目所找的不重复整数）；
  • 10 表示这个数字出现了多次。

那么这 232 个整数，总共所需内存为 232*2b=1GB。因此，当可用内存超过 1GB 时，可以采用位图法。假设内存满足位图法需求，进行下面的操作：

遍历 2.5 亿个整数，查看位图中对应的位，如果是 00，则变为 01，如果是 01 则变为 10，如果是 10 则保持不变。遍历结束后，查看位图，把对应位是 01 的整数输出即可。

当然，本题中特别说明：内存不足以容纳这 2.5 亿个整数，2.5 亿个整数的内存大小为：2.5e8/1024/1024/1024 * 4=3.72GB， 如果内存大于 1GB，是可以通过位图法解决的。

方法总结

判断数字是否重复的问题，位图法是一种非常高效的方法，当然前提是：内存要满足位图法所需要的存储空间。

如何在大量的数据中判断一个数是否存在？

题目描述

给定 40 亿个不重复的没排过序的 unsigned int 型整数，然后再给定一个数，如何快速判断这个数是否在这 40 亿个整数当中？

解答思路

方法一：分治法

依然可以用分治法解决，方法与前面类似，就不再次赘述了。

方法二：位图法

由于 unsigned int 数字的范围是 [0, 1 << 32)，我们用 1<<32=4,294,967,296 个 bit 来表示每个数字。初始位均为 0，那么总共需要内存：4,294,967,296b≈512M。

我们读取这 40 亿个整数，将对应的 bit 设置为 1。接着读取要查询的数，查看相应位是否为 1，如果为 1 表示存在，如果为 0 表示不存在。

方法总结

判断数字是否存在、判断数字是否重复的问题，位图法是一种非常高效的方法。

查找两个大文件共同的URL

题目

给定 a、b 两个文件，各存放 50 亿个 URL，每个 URL 各占 64B，找出 a、b 两个文件共同的 URL。内存限制是 4G。

分析

分治策略

每个 URL 占 64B，那么 50 亿个 URL占用的空间大小约为 320GB。5,000,000,000 * 64B ≈ 320GB

由于内存大小只有 4G，因此，不可能一次性把所有 URL 加载到内存中处理。对于这种类型的题目，一般采用分治策略，即：把一个文件中的 URL 按照某个特征划分为多个小文件，使得每个小文件大小不超过 4G，这样就可以把这个小文件读到内存中进行处理了。

首先遍历文件a，对遍历到的 URL 进行哈希取余 hash(URL) % 1000，根据计算结果把遍历到的 URL 存储到 a0, a1,a2, ..., a999，这样每个大小约为 300MB。使用同样的方法遍历文件 b，把文件 b 中的 URL 分别存储到文件 b0, b1, b2, ..., b999 中。这样处理过后，所有可能相同的 URL 都在对应的小文件中，即 a0 对应 b0, ..., a999 对应 b999，不对应的小文件不可能有相同的 URL。那么接下来，我们只需要求出这 1000 对小文件中相同的 URL 就好了。

接着遍历 ai( i∈[0,999])，把 URL 存储到一个 HashSet 集合中。然后遍历 bi 中每个 URL，看在 HashSet 集合中是否存在，若存在，说明这就是共同的 URL，可以把这个 URL 保存到一个单独的文件中。

前缀树

一般而言，URL 的长度差距不会不大，而且前面几个字符，绝大部分相同。这种情况下，非常适合使用字典树（trie tree） 这种数据结构来进行存储，降低存储成本的同时，提高查询效率。

总结

分治策略：

  1. 分而治之，进行哈希取余；
  2. 对每个子文件进行 HashSet 统计。

前缀树：

  1. 利用字符串的公共前缀来降低存储成本，提高查询效率。

如何在5亿数据中找到中位数？

题目描述

从 5 亿个数中找出中位数。数据排序后，位置在最中间的数就是中位数。当样本数为奇数时，中位数为 第 (N+1)/2 个数；当样本数为偶数时，中位数为 第 N/2 个数与第 1+N/2 个数的均值。

分析

中位数问题可以看做一个统计问题，而不是排序问题，无符号整数大小为4B，则能表示的数的范围为为0 ~ 2^32 - 1（40亿），如果没有限制内存大小，则可以用一个2^32（4GB）大小的数组（也叫做桶）来保存5亿个数中每个无符号数出现的次数。遍历这5亿个数，当元素值等于桶元素索引时，桶元素的值加1。当统计完5亿个数以后，则从索引为0的值开始累加桶的元素值，当累加值等于2.5亿时，这个值对应的索引为中位数。时间复杂度为O(n)。

因为题目要求内存限制512M，所以上述解法不合适。

方法一：双堆法

维护两个堆，一个大顶堆，一个小顶堆。大顶堆中最大的数小于等于小顶堆中最小的数；保证这两个堆中的元素个数的差不超过 1。

若数据总数为偶数，当这两个堆建好之后，中位数就是这两个堆顶元素的平均值。当数据总数为奇数时，根据两个堆的大小，中位数一定在数据多的堆的堆顶。

class MedianFinder {

    private PriorityQueue<Integer> maxHeap;
    private PriorityQueue<Integer> minHeap;

    /** initialize your data structure here. */
    public MedianFinder() {
        maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
        minHeap = new PriorityQueue<>(Integer::compareTo);
    }

    public void addNum(int num) {
        if (maxHeap.isEmpty() || maxHeap.peek() > num) {
            maxHeap.offer(num);
        } else {
            minHeap.offer(num);
        }

        int size1 = maxHeap.size();
        int size2 = minHeap.size();
        if (size1 - size2 > 1) {
            minHeap.offer(maxHeap.poll());
        } else if (size2 - size1 > 1) {
            maxHeap.offer(minHeap.poll());
        }
    }

    public double findMedian() {
        int size1 = maxHeap.size();
        int size2 = minHeap.size();

        return size1 == size2
            ? (maxHeap.peek() + minHeap.peek()) * 1.0 / 2
            : (size1 > size2 ? maxHeap.peek() : minHeap.peek());
    }
}

见 LeetCode No.295：https://leetcode.com/problems/find-median-from-data-stream/

以上这种方法，需要把所有数据都加载到内存中。当数据量很大时，就不能这样了，因此，这种方法适用于数据量较小的情况。

方法二：分治法

下面分享另一种解法（分治法的思想）

分治法的思想是把一个大的问题逐渐转换为规模较小的问题来求解。

对于这道题，顺序读取这 5 亿个数字，对于读取到的数字 num，如果它对应的二进制中最高位为 1，则把这个数字写到 f1 中，否则写入 f0 中。通过这一步，可以把这 5 亿个数划分为两部分，而且 f0 中的数都大于 f1 中的数（最高位是符号位）。

划分之后，可以非常容易地知道中位数是在 f0 还是 f1 中。假设 f1 中有 1 亿个数，那么中位数一定在 f0 中，且是在 f0 中，从小到大排列的第 1.5 亿个数与它后面的一个数的平均值。

提示，5 亿数的中位数是第 2.5 亿与右边相邻一个数求平均值。若 f1 有一亿个数，那么中位数就是 f0 中从第 1.5 亿个数开始的两个数求得的平均值。

对于 f0 可以用次高位的二进制继续将文件一分为二，如此划分下去，直到划分后的文件可以被加载到内存中，把数据加载到内存中以后直接排序，找出中位数。

注意，当数据总数为偶数，如果划分后两个文件中的数据有相同个数，那么中位数就是数据较小的文件中的最大值与数据较大的文件中的最小值的平均值。

如何查询最热门的查询串？

题目描述

搜索引擎会通过日志文件把用户每次检索使用的所有查询串都记录下来，每个查询串的长度不超过 255 字节。

假设目前有 1000w 个记录（这些查询串的重复度比较高，虽然总数是 1000w，但如果除去重复后，则不超过 300w 个）。请统计最热门的 10 个查询串，要求使用的内存不能超过 1G。（一个查询串的重复度越高，说明查询它的用户越多，也就越热门。）

解答思路

每个查询串最长为 255B，1000w 个串需要占用 约 2.55G 内存，因此，我们无法将所有字符串全部读入到内存中处理。

方法一：分治法

分治法依然是一个非常实用的方法。

划分为多个小文件，保证单个小文件中的字符串能被直接加载到内存中处理，然后求出每个文件中出现次数最多的 10 个字符串；最后通过一个小顶堆统计出所有文件中出现最多的 10 个字符串。

方法可行，但不是最好，下面介绍其他方法。

方法二：HashMap 法

虽然字符串总数比较多，但去重后不超过 300w，因此，可以考虑把所有字符串及出现次数保存在一个 HashMap 中，所占用的空间为 300w*(255+4)≈777M（其中，4表示整数占用的4个字节）。由此可见，1G 的内存空间完全够用。

思路如下：

首先，遍历字符串，若不在 map 中，直接存入 map，value 记为 1；若在 map 中，则把对应的 value 加 1，这一步时间复杂度 O(N)。

接着遍历 map，构建一个 10 个元素的小顶堆，若遍历到的字符串的出现次数大于堆顶字符串的出现次数，则进行替换，并将堆调整为小顶堆。

遍历结束后，堆中 10 个字符串就是出现次数最多的字符串。这一步时间复杂度 O(Nlog10)。

方法三：前缀树法

方法二使用了 HashMap 来统计次数，当这些字符串有大量相同前缀时，可以考虑使用前缀树来统计字符串出现的次数，树的结点保存字符串出现次数，0 表示没有出现。

思路如下：

在遍历字符串时，在前缀树中查找，如果找到，则把结点中保存的字符串次数加 1，否则为这个字符串构建新结点，构建完成后把叶子结点中字符串的出现次数置为 1。

最后依然使用小顶堆来对字符串的出现次数进行排序。

方法总结

前缀树经常被用来统计字符串的出现次数。它的另外一个大的用途是字符串查找，判断是否有重复的字符串等。

如何找出排名前 500 的数？

题目描述

有 1w 个数组，每个数组有 500 个元素，并且有序排列。如何在这 10000*500 个数中找出前 500 的数？

方法1

题目中每个数组是排好序的，可以使用归并的方法。

先将第1个和第2个归并，得到500个数据。然后再将结果和第3个数组归并，得到500个数据，以此类推，直到最后找出前500个的数。

方法2

对于这种topk问题，更常用的方法是使用堆排序。

对本题而言，假设数组降序排列，可以采用以下方法：

首先建立大顶堆，堆的大小为数组的个数，即为10000 ，把每个数组最大的值存到堆中。

接着删除堆顶元素，保存到另一个大小为 500 的数组中，然后向大顶堆插入删除的元素所在数组的下一个元素。

重复上面的步骤，直到删除完第 500 个元素，也即找出了最大的前 500 个数。

示例代码如下：

import lombok.Data;

import java.util.Arrays;
import java.util.PriorityQueue;

@Data
public class DataWithSource implements Comparable<DataWithSource> {
    /**
     * 数值
     */
    private int value;

    /**
     * 记录数值来源的数组
     */
    private int source;

    /**
     * 记录数值在数组中的索引
     */
    private int index;

    public DataWithSource(int value, int source, int index) {
        this.value = value;
        this.source = source;
        this.index = index;
    }

    /**
     *
     * 由于 PriorityQueue 使用小顶堆来实现，这里通过修改
     * 两个整数的比较逻辑来让 PriorityQueue 变成大顶堆
     */
    @Override
    public int compareTo(DataWithSource o) {
        return Integer.compare(o.getValue(), this.value);
    }
}


class Test {
    public static int[] getTop(int[][] data) {
        int rowSize = data.length;
        int columnSize = data[0].length;

        // 创建一个columnSize大小的数组，存放结果
        int[] result = new int[columnSize];

        PriorityQueue<DataWithSource> maxHeap = new PriorityQueue<>();
        for (int i = 0; i < rowSize; ++i) {
            // 将每个数组的最大一个元素放入堆中
            DataWithSource d = new DataWithSource(data[i][0], i, 0);
            maxHeap.add(d);
        }

        int num = 0;
        while (num < columnSize) {
            // 删除堆顶元素
            DataWithSource d = maxHeap.poll();
            result[num++] = d.getValue();
            if (num >= columnSize) {
                break;
            }

            d.setValue(data[d.getSource()][d.getIndex() + 1]);
            d.setIndex(d.getIndex() + 1);
            maxHeap.add(d);
        }
        return result;

    }

    public static void main(String[] args) {
        int[][] data = {
                {29, 17, 14, 2, 1},
                {19, 17, 16, 15, 6},
                {30, 25, 20, 14, 5},
        };

        int[] top = getTop(data);
        System.out.println(Arrays.toString(top)); // [30, 29, 25, 20, 19]
    }
}

如何按照 query 的频度排序？

题目描述

有 10 个文件，每个文件大小为 1G，每个文件的每一行存放的都是用户的 query，每个文件的 query 都可能重复。要求按照 query 的频度排序。

解答思路

如果 query 的重复度比较大，可以考虑一次性把所有 query 读入内存中处理；如果 query 的重复率不高，那么可用内存不足以容纳所有的 query，这时候就需要采用分治法或其他的方法来解决。

方法一：HashMap 法

如果 query 重复率高，说明不同 query 总数比较小，可以考虑把所有的 query 都加载到内存中的 HashMap 中。接着就可以按照 query 出现的次数进行排序。

方法二：分治法

分治法需要根据数据量大小以及可用内存的大小来确定问题划分的规模。对于这道题，可以顺序遍历 10 个文件中的 query，通过 Hash 函数 hash(query) % 10 把这些 query 划分到 10 个小文件中。之后对每个小文件使用 HashMap 统计 query 出现次数，根据次数排序并写入到零外一个单独文件中。

接着对所有文件按照 query 的次数进行排序，这里可以使用归并排序（由于无法把所有 query 都读入内存，因此需要使用外排序）。

方法总结

  • 内存若够，直接读入进行排序；
  • 内存不够，先划分为小文件，小文件排好序后，整理使用外排序进行归并。

5亿个数的大文件怎么排序？

问题

给你1个文件bigdata，大小4663M，5亿个数，文件中的数据随机，一行一个整数：

6196302
3557681
6121580
2039345
2095006
1746773
7934312
2016371
7123302
8790171
2966901
...
7005375

现在要对这个文件进行排序，怎么做？

内部排序

先尝试内排，选2种排序方式：

3路快排：

private final int cutoff = 8;

public <T> void perform(Comparable<T>[] a) {
		perform(a,0,a.length - 1);
	}

	private <T> int median3(Comparable<T>[] a,int x,int y,int z) {
		if(lessThan(a[x],a[y])) {
			if(lessThan(a[y],a[z])) {
				return y;
			}
			else if(lessThan(a[x],a[z])) {
				return z;
			}else {
				return x;
			}
		}else {
			if(lessThan(a[z],a[y])){
				return y;
			}else if(lessThan(a[z],a[x])) {
				return z;
			}else {
				return x;
			}
		}
	}

	private <T> void perform(Comparable<T>[] a,int low,int high) {
		int n = high - low + 1;
		//当序列非常小，用插入排序
		if(n <= cutoff) {
			InsertionSort insertionSort = SortFactory.createInsertionSort();
			insertionSort.perform(a,low,high);
			//当序列中小时，使用median3
		}else if(n <= 100) {
			int m = median3(a,low,low + (n >>> 1),high);
			exchange(a,m,low);
			//当序列比较大时，使用ninther
		}else {
			int gap = n >>> 3;
			int m = low + (n >>> 1);
			int m1 = median3(a,low,low + gap,low + (gap << 1));
			int m2 = median3(a,m - gap,m,m + gap);
			int m3 = median3(a,high - (gap << 1),high - gap,high);
			int ninther = median3(a,m1,m2,m3);
			exchange(a,ninther,low);
		}

		if(high <= low)
			return;
		//lessThan
		int lt = low;
		//greaterThan
		int gt = high;
		//中心点
		Comparable<T> pivot =  a[low];
		int i = low + 1;

		/*
		* 不变式：
		*	a[low..lt-1] 小于pivot -> 前部(first)
		*	a[lt..i-1] 等于 pivot -> 中部(middle)
		*	a[gt+1..n-1] 大于 pivot -> 后部(final)
		*
		*	a[i..gt] 待考察区域
		*/

		while (i <= gt) {
			if(lessThan(a[i],pivot)) {
				//i-> ,lt ->
				exchange(a,lt++,i++);
			}else if(lessThan(pivot,a[i])) {
				exchange(a,i,gt--);
			}else{
				i++;
			}
		}

		// a[low..lt-1] < v = a[lt..gt] < a[gt+1..high].
		perform(a,low,lt - 1);
		perform(a,gt + 1,high);
	}

归并排序：

	/**
	 * 小于等于这个值的时候，交给插入排序
	 */
	private final int cutoff = 8;

	/**
	 * 对给定的元素序列进行排序
	 *
	 * @param a 给定元素序列
	 */
	@Override
	public <T> void perform(Comparable<T>[] a) {
		Comparable<T>[] b = a.clone();
		perform(b, a, 0, a.length - 1);
	}

	private <T> void perform(Comparable<T>[] src,Comparable<T>[] dest,int low,int high) {
		if(low >= high)
			return;
			
		//小于等于cutoff的时候,交给插入排序
		if(high - low <= cutoff) {
			SortFactory.createInsertionSort().perform(dest,low,high);
			return;
		}

		int mid = low + ((high - low) >>> 1);
		perform(dest,src,low,mid);
		perform(dest,src,mid + 1,high);

		//考虑局部有序 src[mid] <= src[mid+1]
		if(lessThanOrEqual(src[mid],src[mid+1])) {
			System.arraycopy(src,low,dest,low,high - low + 1);
		}

		//src[low .. mid] + src[mid+1 .. high] -> dest[low .. high]
		merge(src,dest,low,mid,high);
	}
	
	private <T> void merge(Comparable<T>[] src,Comparable<T>[] dest,int low,int mid,int high) {

		for(int i = low,v = low,w = mid + 1; i <= high; i++) {
			if(w > high || v <= mid && lessThanOrEqual(src[v],src[w])) {
				dest[i] = src[v++];
			}else {
				dest[i] = src[w++];
			}
		}
	}

数据太多，递归太深，会导致栈溢出。数据太多，数组太长，会导致OOM。

可见这两种方式不适用。

位图法

BitMap算法的核心思想是用bit数组来记录0-1两种状态，然后再将具体数据映射到这个比特数组的具体位置，这个比特位设置成0表示数据不存在，设置成1表示数据存在。

BitMap算在在大量数据查询、去重等应用场景中使用的比较多，这个算法具有比较高的空间利用率。

实现代码如下：

private BitSet bits;

public void perform(
    String largeFileName,
    int total,
    String destLargeFileName,
    Castor<Integer> castor,
    int readerBufferSize,
    int writerBufferSize,
    boolean asc) throws IOException {

    System.out.println("BitmapSort Started.");
    long start = System.currentTimeMillis();
    bits = new BitSet(total);
    InputPart<Integer> largeIn = PartFactory.createCharBufferedInputPart(largeFileName, readerBufferSize);
    OutputPart<Integer> largeOut = PartFactory.createCharBufferedOutputPart(destLargeFileName, writerBufferSize);
    largeOut.delete();

    Integer data;
    int off = 0;
    try {
        while (true) {
            data = largeIn.read();
            if (data == null)
                break;
            int v = data;
            set(v);
            off++;
        }
        largeIn.close();
        int size = bits.size();
        System.out.println(String.format("lines : %d ,bits : %d", off, size));

        if(asc) {
            for (int i = 0; i < size; i++) {
                if (get(i)) {
                    largeOut.write(i);
                }
            }
        }else {
            for (int i = size - 1; i >= 0; i--) {
                if (get(i)) {
                    largeOut.write(i);
                }
            }
        }

        largeOut.close();
        long stop = System.currentTimeMillis();
        long elapsed = stop - start;
        System.out.println(String.format("BitmapSort Completed.elapsed : %dms",elapsed));
    }finally {
        largeIn.close();
        largeOut.close();
    }
}

private void set(int i) {
    bits.set(i);
}

private boolean get(int v) {
    return bits.get(v);
}

外部排序

什么是外部排序？

  1. 内存极少的情况下，利用分治策略，利用外存保存中间结果，再用多路归并来排序;

实现原理如下：

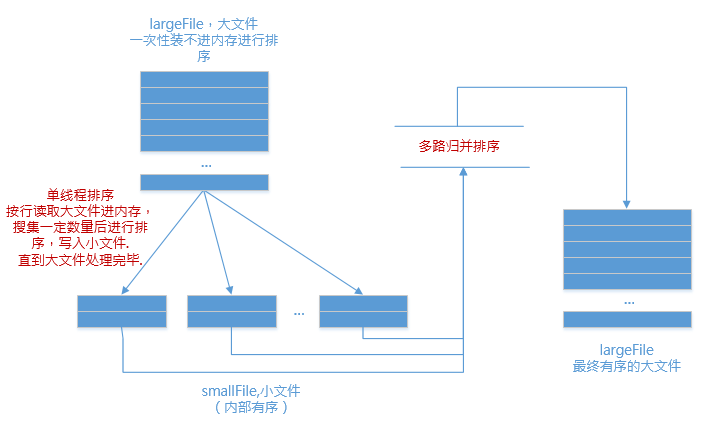
1.分成有序的小文件

内存中维护一个极小的核心缓冲区memBuffer，将大文件bigdata按行读入，搜集到memBuffer满或者大文件读完时，对memBuffer中的数据调用内排进行排序，排序后将有序结果写入磁盘文件bigdata.xxx.part.sorted.
循环利用memBuffer直到大文件处理完毕，得到n个有序的磁盘文件：

2.合并成1个有序的大文件

现在有了n个有序的小文件，怎么合并成1个有序的大文件？

利用如下原理进行归并排序：

举个简单的例子：

文件1：3,6,9。
文件2：2,4,8。
文件3：1,5,7。

第一回合：
文件1的最小值：3 , 排在文件1的第1行。
文件2的最小值：2，排在文件2的第1行。
文件3的最小值：1，排在文件3的第1行。
那么，这3个文件中的最小值是：min(1,2,3) = 1。
也就是说，最终大文件的当前最小值，是文件1、2、3的当前最小值的最小值。
上面拿出了最小值1，写入大文件。

第二回合：
文件1的最小值：3 , 排在文件1的第1行。
文件2的最小值：2，排在文件2的第1行。
文件3的最小值：5，排在文件3的第2行。
那么，这3个文件中的最小值是：min(5,2,3) = 2。
将2写入大文件。

也就是说，最小值属于哪个文件，那么就从哪个文件当中取下一行数据。（因为小文件内部有序，下一行数据代表了它当前的最小值）

感兴趣的小伙伴可以自己尝试去实现下~